Burrows-Wheeler transform (or, BWT) is a block compression algorithm and is used in programs like bzip. The output of the algorithm is a string which contains chunks of same characters which can be easily stored in a compact form. The compression is lossless, that is, we can get back the exact original string from the compressed format. The way it works is pretty amazing.
The Algorithm
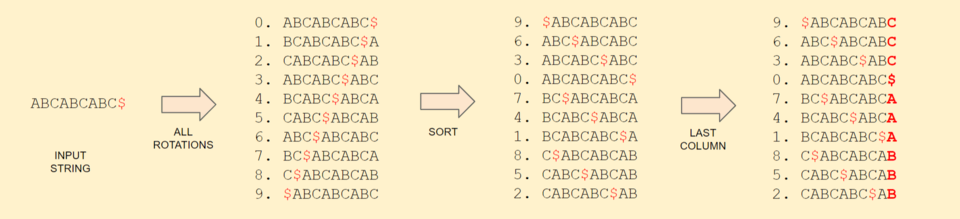
The algorithm is very simple, you just sort all the rotations lexicographically and take the last column of it. This last column is the Burrows-Wheeler transform of the string. An example will make it clear. Let our string be “PANAMABANANA”. We will add a $ at the end of the string, this end character should not be anywhere in the original string. (Considering $ to be the smallest character).

The final transformed string we get is “ANMNNBPAAAAA$”. This is the BWT of our original string. Compression? Here, we can see that we get chunks of same characters, like 5 A’s. We can store it as “ANM2NBP5A$”. For some strings we can get even more characters together in a continuous run, resulting in better compression. Great! So, do we always get same characters together? NO. For example:

“AC$BCDABDBADC”. Here none of the characters is together. Nothing to compress. Worse than the original string. Let’s see another example.
“3C$3A3B”. Isn’t it nice? Hmm… So when do we get repeated characters? Well, if there are substrings which occur often in the string (like in “ABCABCABC”), then there will be more characters together. This turns out to be great for compressing strings with repeats, like the DNA sequences, where we have only 4 characters (A, C, G, T) and a lot of repeated patterns.
Great, we got our string compressed. But how to get back original string from this transform?
Inverse
All the information required for getting back the original string from it’s BWT is available in the BWT itself (the last column). First, let’s look at an important fact about the first column and last column(BWT) of the sorted rotations.
For any character x, the ith x in the first column corresponds to the ith x in the last column!
For example, in the “PANAMABANANA” example, the 2nd A in first column and the 2nd A in last column are the same A. Similarly, the 3rd N in first column and 3rd N in last column is same.

This will hold true for any character, always. You can verify yourself why that’s true.
Now to get back our string, we can start tracing character by character using last column(BWT) and first column. We can get the first column by sorting the last column (BWT of the string) (actually, you just need to count the occurrence of each character). We will start tracing from $ since we know that it’s the last character. For ith x in last column, we will go to ith x in first column. Record that character. Get the corresponding indexed character in last column and repeat. Keep doing till we hit the $.
Let’s do it on a small example, “RAGA”. First it’s transformation:

Now it’s inverse transformation. Start by $. This is the first $ in the last column, so we go to the first $ in the first column, i.e. first row. Refer to the figure below. We get an A here. This is the first A in last column, so we go to first A in first column. Corresponding to it we get G. This is the first G, so we go to first G in first column, for which we get an A. This is second A in last column, going to second A in first column, we get R. This is the first R in last column, we go to first R in first column. We get a $ and we stop. This image will make the steps clear:
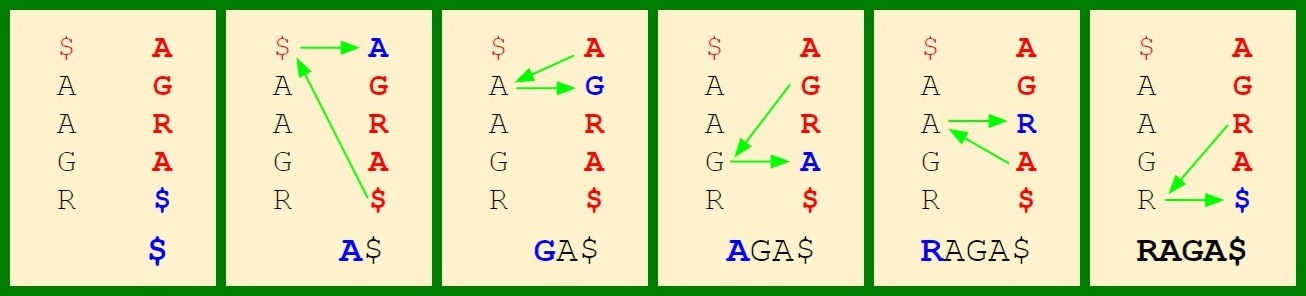
Tada! We got back our original string “RAGA”!
You can try out inverting other examples given in this post.
That’s it for this post. BWT is used in bzip and bzip2 for compression. BWT is also used for read alignment, where you have a lot of short query strings (known as reads) and you have to find whether it’s a substring of a larger reference string. That’s called Burrows-Wheeler Alignment.
Extras
- Original technical report of Burrows-Wheeler Transform (1994).
- Google developers have a video on Burrows-Wheeler Transform, Watch it on youtube.
- You can try BWT on this online tool.