Consider the following problem of read alignment. You are given millions of small pieces of DNA sequence, called reads and one large DNA sequence called the reference sequence (DNA sequences contain only 4 letters A, C, G, T representing the four bases). You have to find how many of those reads matches the reference sequence and at what positions. In simplified form, you have many shorter strings to be matched against a single very large string. How can we do it fast?
Well, it’s a string matching problem. But the size of one string is very large (billions of characters) and all other strings are to be matched against this one string. Can we do some preprocessing so that the time complexity of matching depends only on the length of shorter strings and not on the longer one?
In this post, we will be solving this read alignment problem by using the Burrows-Wheeler transform of the reference sequence. Since the problem is mostly used in read alignment in DNA sequences, I will be using strings with characters A, C, G and T only.
First, let me define a function:
Rank (c, i) : tells how many times character c appeared before index i.
Example,
string: C G T A A C G G T
index: 0 1 2 3 4 5 6 7 8
Rank(G, 3) = 1
Rank(G, 7) = 2
Rank(G, 8) = 3
Now let’s look how this algorithm works. First, we create the BWT of the reference sequence: CGATGCACCGGT (post on BWT). Along with the BWT, we also store the suffix array, i.e. the mapping of each character in BWT to the rotation it came from.
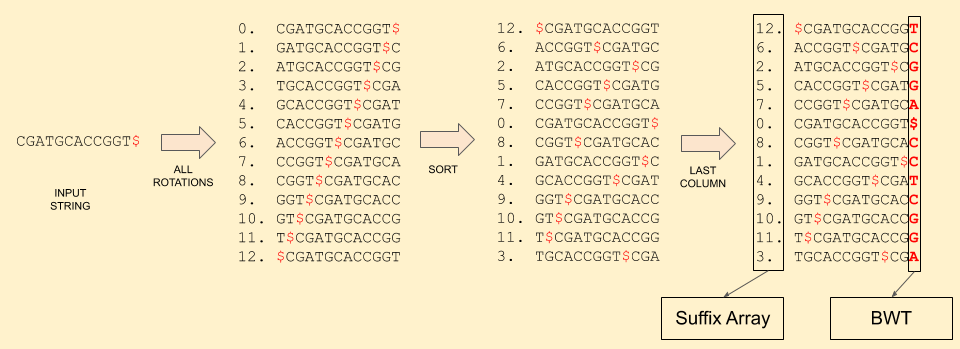
Notice that the sorted rotations matrix contains all the possible suffix of the string. And the suffix array tells the starting index of that suffix.
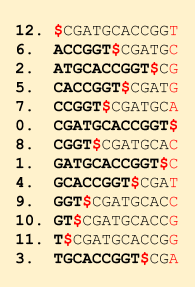
Now with all this data structure created and the Rank() function implemented, we are ready to search a query string. The overall idea is that we start from the last character in the query string and keep moving towards the start and in each move, we reduce the possible positions where we can find a match. Recall the first-last property of BWT that for any character x, the ith x in the first column is the ith x in the last column. We can easily get the first column by sorting the BWT (just need to count the occurrence of each character). Let’s say we have m A’s and k C’s in the BWT of the reference string. The first column will be like (remember that first column is sorted, so first comes $, then all A’s, then all C’s, then G’s and then all the T’s):
$ A . . . A C . . . C G . . .
0 1 - - - m m+1 - - n - - - -
where, n = m + k
The C’s lie in this band of indices starting from m+1 up to m+k. If we have to search for character C, we need to search in this band. Let our read be ending in …AC. Then we can start with the band (m+1, m+k). Our next character is A (remember we are traversing the read backwards), so we then compute p = Rank (A, m+1) and q = Rank (A, m+k) in the BWT. These 2 numbers tell us the number of A’s before the start index of the band and the number of A’s before the end index of the band, respectively. Notice that all these A’s actually have a C after them in the reference string.

By these ranks, we get to know which A’s are a potential match. We need to now search only at these A’s. Now we can reduce our search band to (1+p, 1+q). (1 is the start of A band in the first column). All these will be having an A followed by a C.
We can now jump to the next character just before A and repeat this process. We stop when we hit the start of the read string or the band size reduces to zero, indicating that no match exists.
Let’s follow through an example:
Reference sequence: C G A T G C A C C G G T $
Burrows-Wheeler: T C G G A $ C C T C G G A
Suffix Array: 12 6 2 5 7 0 8 1 4 9 10 11 3
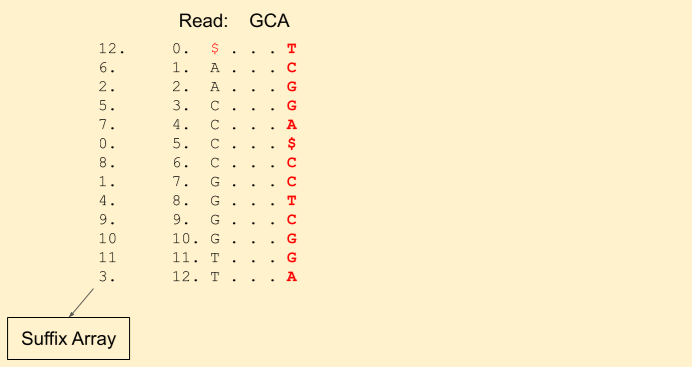
Let the read to be matched be: GCA. We start from the last character A. We get our first band (1, 3) (including 1, but excluding 3, i.e indices {1, 2}).
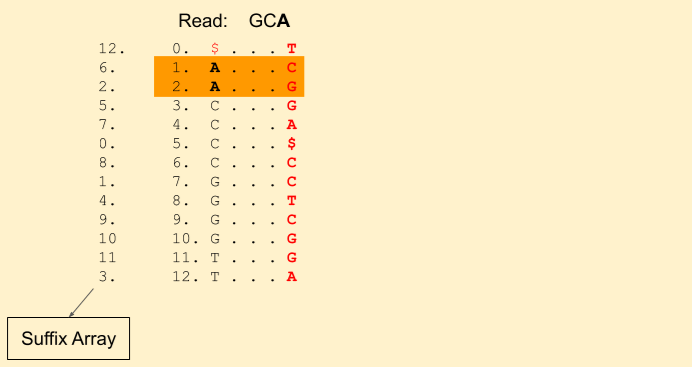
Next character in the read is C (remember, we are moving backwards). We find Rank(C, 1) = 0 and Rank(C, 3) = 1. This tells that there is just one C in the current band. Our new band now is (3+0, 3+1) = (3, 4) (i.e. indices {3}). Our band size has been reduced to 1. That means, there is still a chance we will find a match. If it was gone to 0, then that means there is no match.
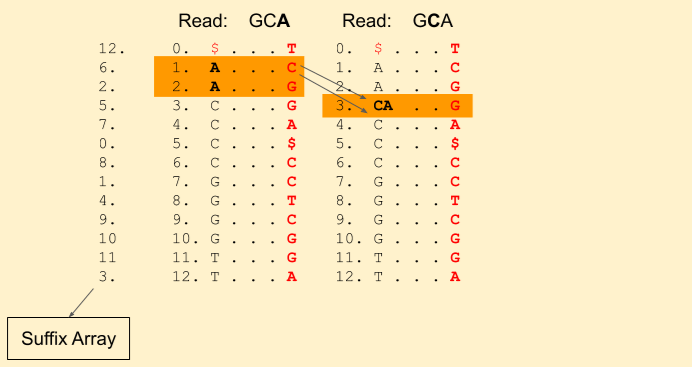
Next we have a G in the read. We find Rank(G, 3) = 1 and Rank(G, 4) = 2. And update our band to (7+1, 7+2) = (8, 9).
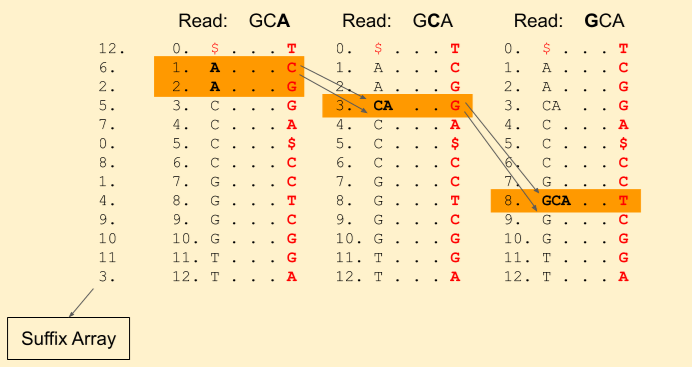
We hit the end of the read. Voila! we found a match. We can get the index from the suffix array, i.e. 4.
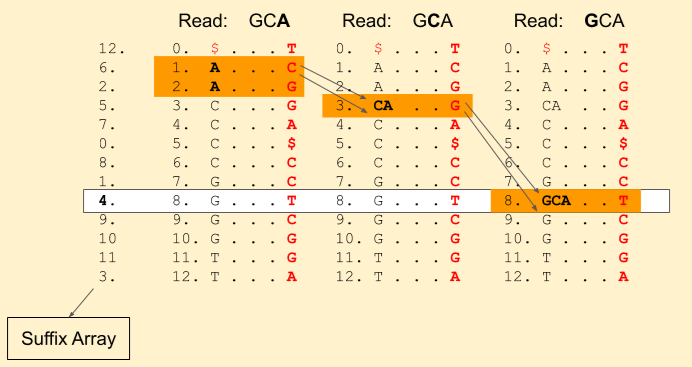
Reference sequence: C G A T G C A C C G G T $ Index: 0 1 2 3 4 5 6 7 8 . . . .
If there were more than one matches, the band size would have been more than one, and all those indices would be a match. If there were none, the band size would have reduced to zero. Pretty simple, right?
We can write up a recursive pseudo-code for this (it need not to be recursive, but this will help when we’ll code for mismatches):
BWA(band_start, band_end, read, index):
if(index == -1):
return band_start, band_end
if(band_start == band_end):
return NO MATCH
s = read[index]
rank_top = Rank(s, band_start)
rank_bottom = Rank(s, band_end)
return BWA(bands[s] + rank_top, bands[s] + rank_bottom, read, index-1)
The initial call is based on the last character. And the bands array holds the starting indices for each character, e.g. for strings with only A, C, G, T:
bands['A'] = 1
bands['C'] = 1 + count(A)
bands['G'] = 1 + count(A) + count(C)
bands['T'] = 1 + count(A) + count(C) + count(G)
From the band indices that we got, we can get the position where we found a match using the prefix array.
That’s it for this post. I appreciate your patience for reading until the end. In the next post, we’ll discuss how we can also handle mismatches, i.e. the query string does match exactly but with a few characters wrongly matched.